Roof Pitch Angles Calculator - app and formulas for calculating degrees in metric and imperial system
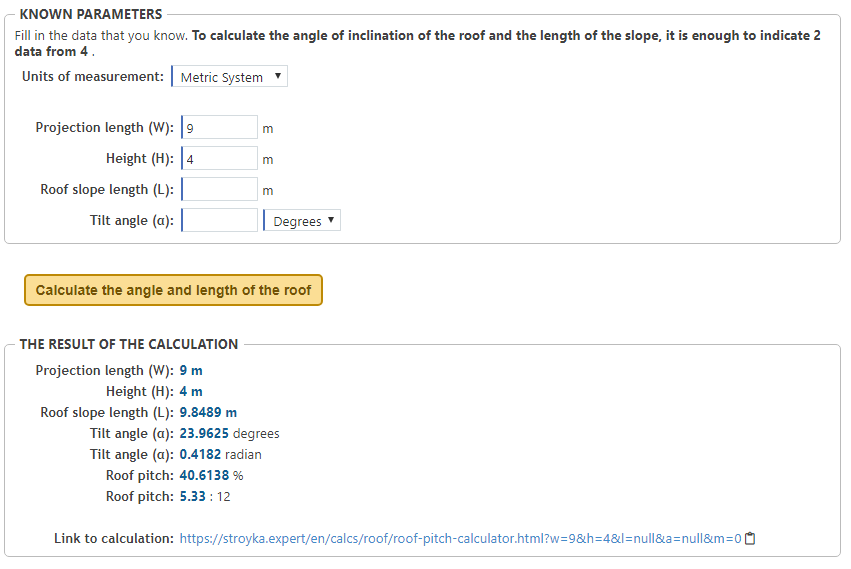
Roof pitch angle calculator - briefly about the calculation
The roof pitch angle calculator is used to calculate both the roof slope angle and the missing roof data — the projection, height, length, and slope angle of the roof. Visually, where and what values can be seen in the drawing of the calculator, which is under the form of calculation.
To calculate the angle of the roof or the data, it is enough to specify only two known values, and other values (if any) can be used for testing.
Roof pitch calculator app
Roof pitch angle in degrees and slope length formulas
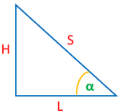
In the picture: a - slope angle, S - roof slope length, H - roof height in the upper part, L - roof slope projection length
Accordingly, all quantities can be found:- a = arctg(H/L) or a = arcsin(H/S)
- H = L * tg a
- S = H / sin a
The above formulas allow you to determine roof pitch (if for some reason our roof pitch calculator did not fit you)
Roof pitch degree table
| Roof pitch degree table | |
| 1-12 | 4.76° |
| 2-12 | 9.46° |
| 3-12 | 14.04° |
| 4-12 | 18.43° |
| 5-12 | 22.62° |
| 6-12 | 26.57° |
| 7-12 | 30.26° |
| 8-12 | 33.69° |
| 9-12 | 36.87° |
| 10-12 | 39.81° |
| 11-12 | 42.51° |
| 12-12 | 45° |
Historical roof pitches
Historically, roof pitch was designated in two other ways: A ratio of the ridge height to the width of the building (span) and as a ratio of the rafter length to the width of the building.
Commonly used roof pitches were given names such as:
- Greek: the ridge height is 1/9 to 1/7th the span (an angle of 12.5° to 16°)
- Roman: the ridge height is 2/9ths to 1/3 the span (an angle of 24° to 34°)
- Common: the rafter length is 3/4 the span (about 48°)
- Gothic: the rafters equal the span (60°)
- Elizabethan: the rafters are longer than the span (more than 60°)